八大经典排序
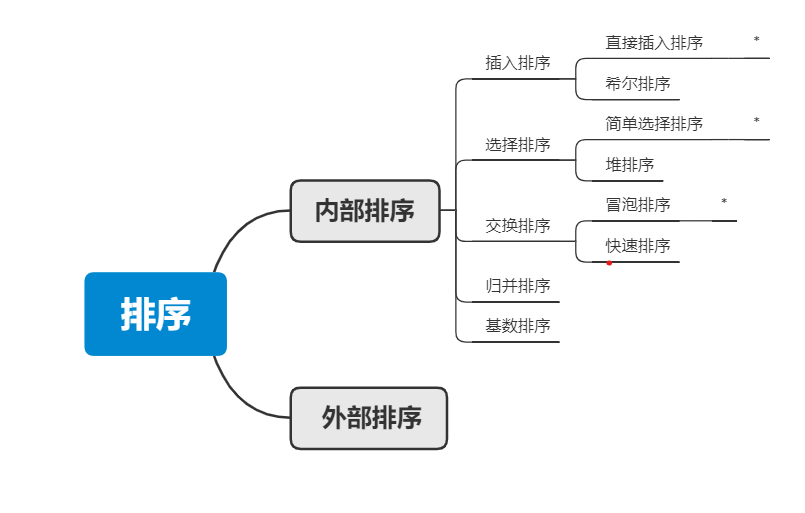
1、冒泡排序
基本介绍:冒泡排序是一种交换排序
基本思想:(假定从小到大的顺序)从第一个元素开始,相邻两个数据进行比较,将小的值放在左边。第一轮:从第一个元素开始,和与其相邻的后一个元素进行比较,
若后一个比前一个小,则交换位置,否则不变,然后两个索引都向后移动一位,继续判断至最后一组数据,第二轮:从第二个元素出发,继续重复上述进行比较、换位,
再进行下一轮比较,直到最后一轮结束。
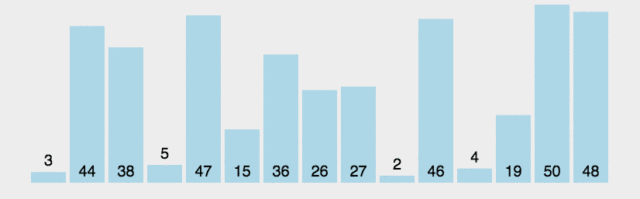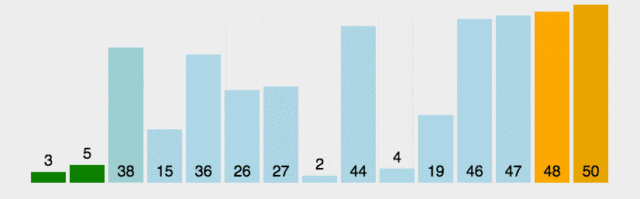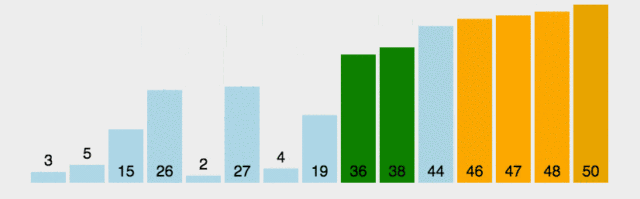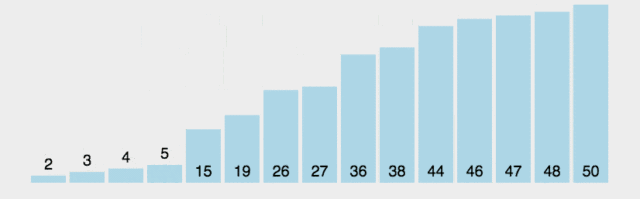
时间复杂度:O(n2),通过测试,长度为80000的数组,数组中的元素从0-800000随机赋值,运行时间为6s;
代码实现:
public static void selectX(int[] arr){ for (int i = 0; i < arr.length - 1; i++) { for (int j = i + 1; j < arr.length; j++) { if(arr[i] > arr[j]){ int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } } }
2、简单选择排序
基本介绍: 选择排序也属于内部排序;与堆排序共为选择排序
基本思想: (也是假定从小到大的顺序) 先设定第一个元素为最小,让其后边的每个元素都与其判断,保存最小的数据和最小数据的索引位置,
在一轮判断后将最小值与第一个元素做替换,再设定第二个元素为当前最小值,继续判断,直到最后一组结束。

时间复杂度:O(n2),通过测试,长度为80000的数组,数组中的元素从0-800000随机赋值,运行时间不到1s;
代码实现:
public static void select2(int[] arr) { // 80000 : 不到一秒 // 800000 : 一分钟 int minIndex = 0; int min = arr[minIndex]; for(int i = 0; i < arr.length - 1; i++) { for(int j = i + 1; j < arr.length;j++) { if(arr[j] < min) { min = arr[j]; minIndex = j; } } if(minIndex != i) { arr[minIndex] = arr[i]; arr[i] = min; } } }
3、简单插入排序
基本介绍:插入排序也属于内部排序;与希尔排序同为插入排序
基本思路:(小->大)先假定有两个数组,无序数组和有序数组,将无序数组中的一个元素与有序中的元素一一比较,找出合适的位置后插入进去。
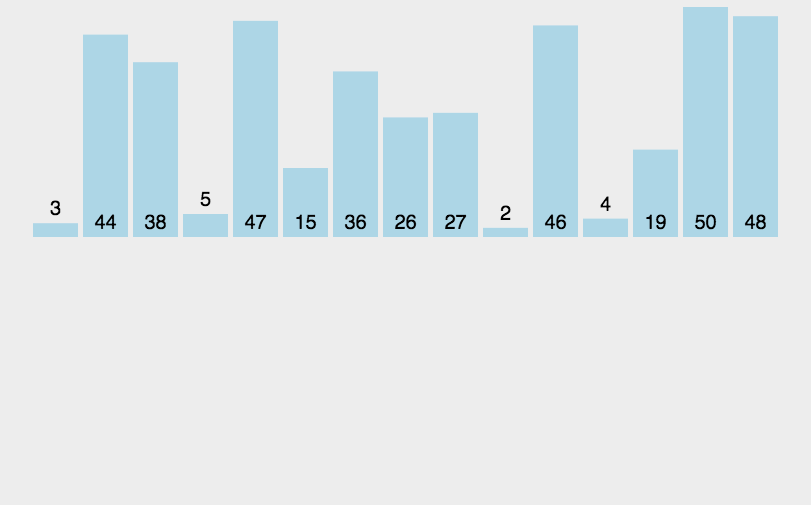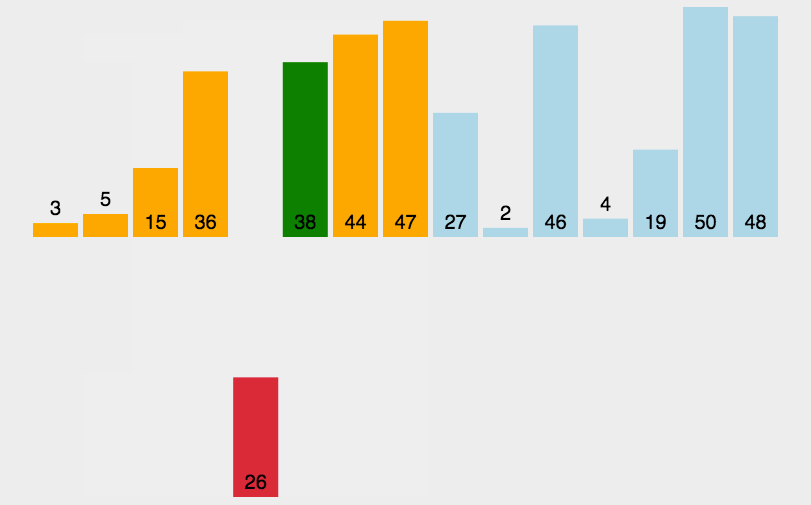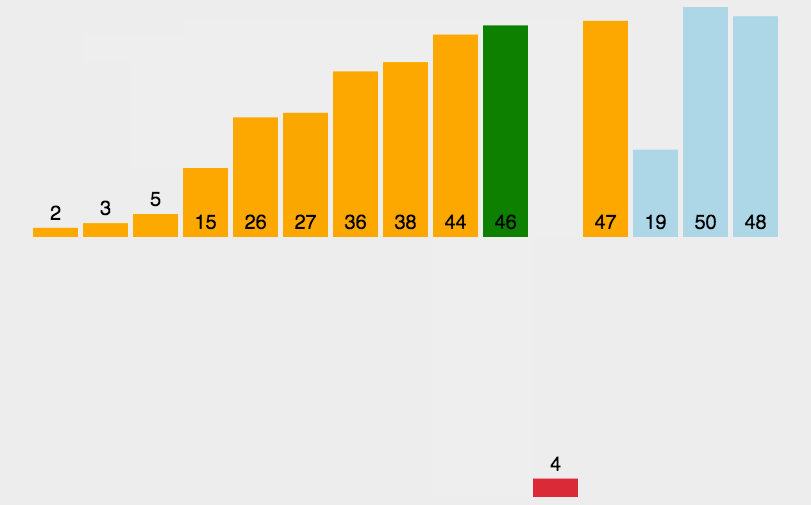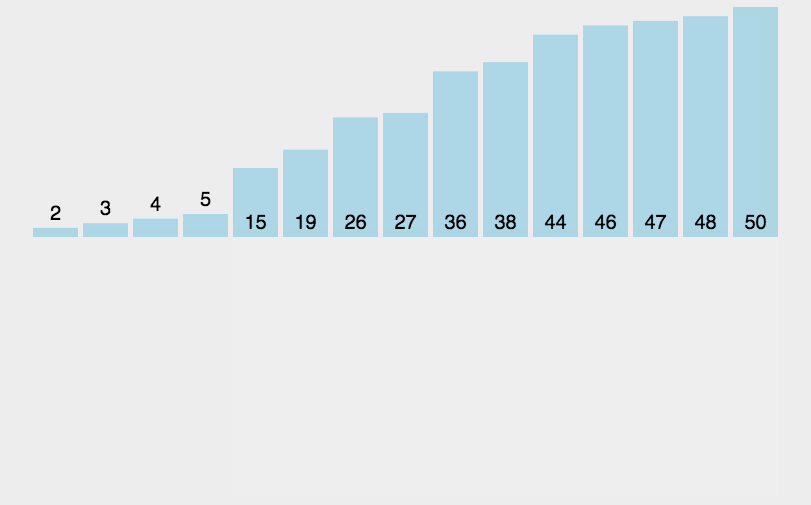
时间复杂度: O(n2),通过测试,长度为80000的数组,数组中的元素从0-800000随机赋值,运行时间不到1s;
代码实现 :
public static void insert(int[] arr) { for(int i = 1; i < arr.length ; i++) { int insertIndex = i - 1; int insertVal = arr[i]; while(insertIndex >= 0 && insertVal < arr[insertIndex]) { //找插入的地方 arr[insertIndex + 1] = arr[insertIndex]; //逐个往后移一位, insertIndex--; } arr[insertIndex + 1] = insertVal; //找到了小的数放的位置 } }
4、希尔排序 (插入排序)
基本介绍:希尔排序是插入排序的一种。
基本思路: 希尔排序是将一个数组先分成长度/2组数据,同一组数据相邻间距为长度/2,根据交换法或位移法将数据进行交换,交换完后再将数据分为间距/2组数据,
每一组之间继续进行比较交换,直到间距为0,即为结束。
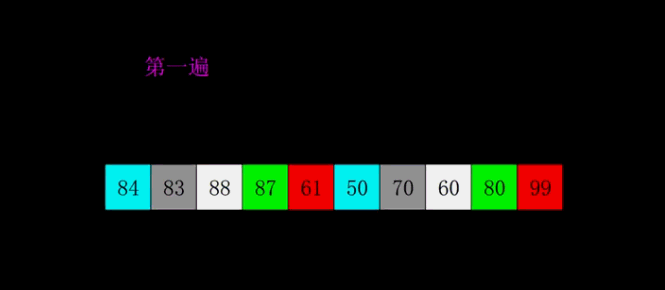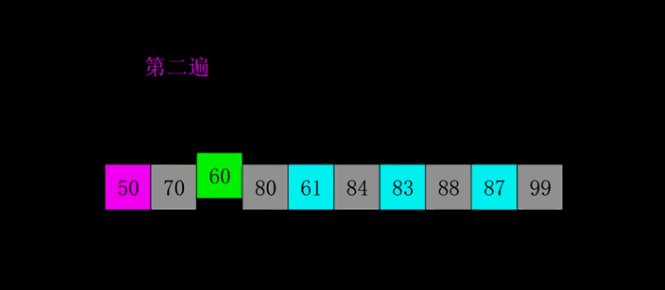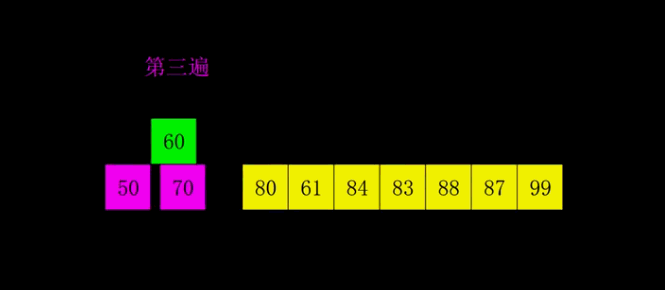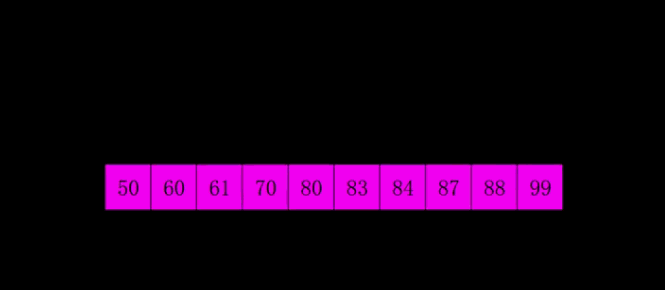
时间复杂度:O(n2) 通过测试, 交换法 8万数据 4s; 位移法 80万数据 不到1s 800万数据2s, 显然希尔位移法排序效率更高。
代码实现:
//交换法 public static void shellSort(int[] arr) { // 八万 : 4s int count = 0; int temp = 0; for(int gsp = arr.length / 2; gsp > 0; gsp /= 2) { for(int i = gsp; i < arr.length; i++) { for(int j = i - gsp; j > 0; j -= gsp) { if(arr[j] > arr[j + gsp]) { temp = arr[j]; arr[j] = arr[j + gsp]; arr[j + gsp] = temp; } } } } } //移位法 public static void shellSort2(int[] arr) { // 8000000 两秒 for(int gap = arr.length / 2; gap > 0; gap /= 2) { for(int i = gap; i < arr.length; i++) { int j = i; int temp = arr[j]; while(j - gap > 0 && temp < arr[j - gap]) { arr[j] = arr[j - gap]; j -= gap; } arr[j] = temp; } } }
5、快速排序
基本介绍:快速排序是对冒泡排序的一种改进。
基本思想:通过一趟排序,将数据分为以某个值大小为界限的两部分,再将这两部分值分别以以上方式继续分组,直到数据变为有序。此方法可以用递归调用,用空间换时间,
大大提高了排序所耗费的时间。

时间复杂度:O(n*logn) 80万数据 不到1s 800万数据2s
代码实现:
public static void quick(int[] arr,int lift,int right) { if(lift < right) { int l = lift; int r = right; int key = arr[l]; while(l < r) { while(l < r && arr[r] >= key) { r -= 1; } arr[l] = arr[r]; while(l < r && arr[l] <= key) { l += 1; } arr[r] = arr[l]; //这里可能已经完成,因此赋值需要移位** if(l < r) { arr[r--] = arr[l]; } } arr[l] = key; //左向递归 quick(arr,lift,l - 1); //右向递归 quick(arr,l + 1,right); } }
6、归并排序
基本介绍:归并排序用到了分治策略,先将数组分解成一个个小的数组,然后再将数组进行排序整合,变成一个有序的大数组。
基本思想:用递归的方法将一个长的数组分解成一个个小的数组,然后给每个分解过的数组再进行排序操作,直到完成排序。
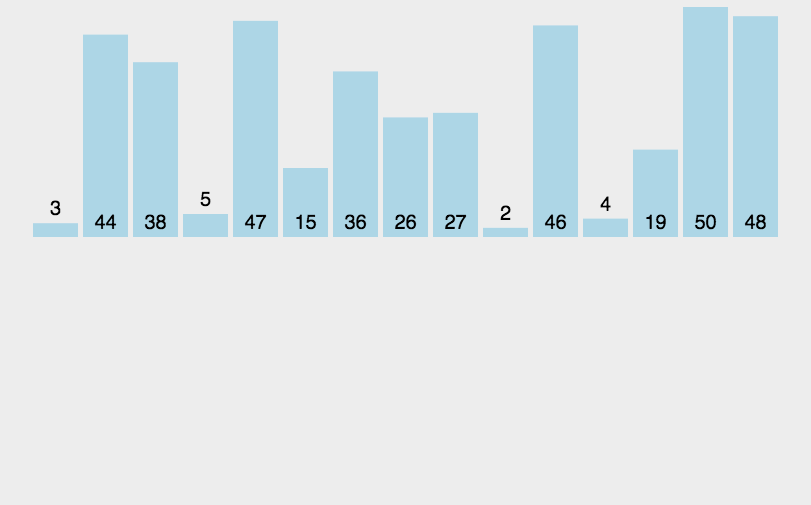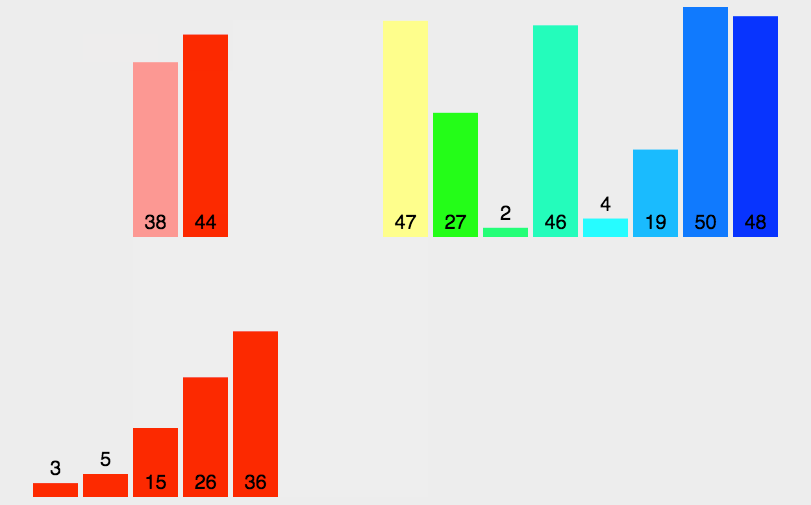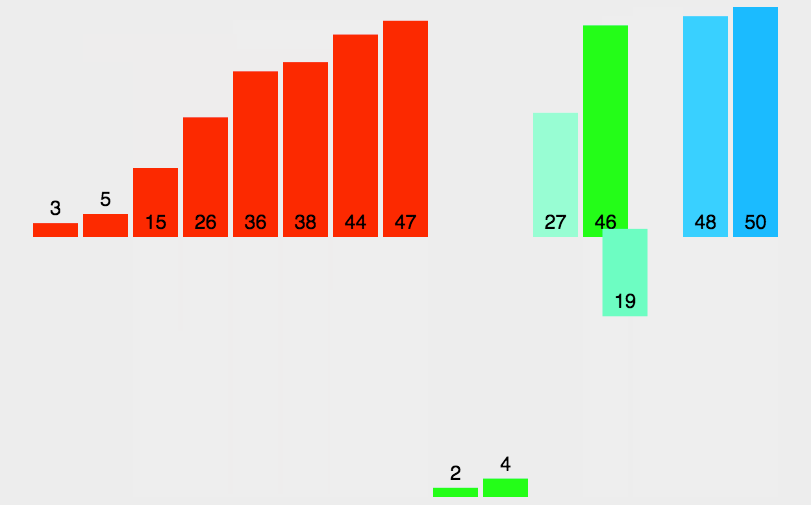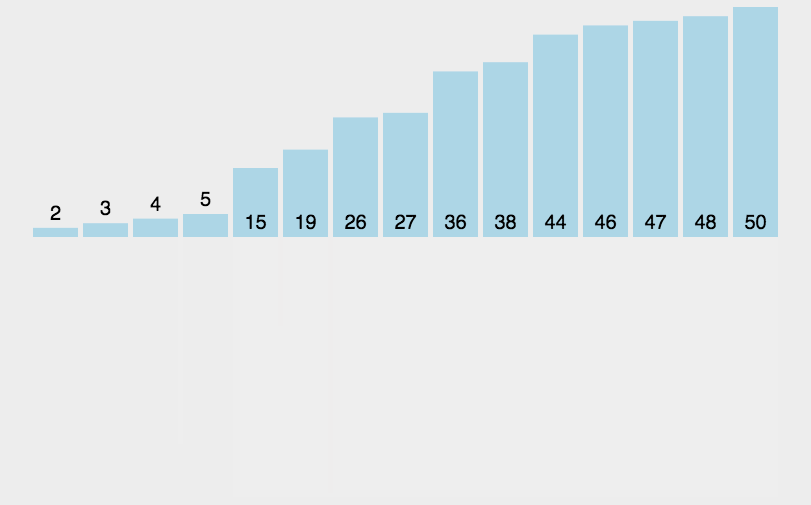
时间复杂度:O(nlog2) 800万个数据只用了不到一秒的时间
代码实现:
//分: 提供分解数组的方法 public static void merge(int[] arr, int left, int right,int[] temp) { if(left < right) { int mid = (left + right) / 2; //左分 merge(arr, left, mid, temp); //右分 merge(arr, mid + 1, right, temp); mergeSort(arr,left,right,mid,temp); } } //治: 提供合数组的方法 public static void mergeSort(int arr[], int left, int right, int mid, int temp[]) { if(left < right) { int i = left; int j = mid + 1; //temp临时的索引 int t = 0; //三大步骤进行合并 //1.先将两个部分的数组比较后放入临时数组中,直到其中一个数组放完 while(i <= mid && j <= right) { if(arr[i] <= arr[j]) { temp[t] = arr[i]; i += 1; t += 1; }else { temp[t] = arr[j]; j += 1; t += 1; } } //2.再将另一个没放完的数组全部放入临时数组中 while(i <= mid) { temp[t] = arr[i]; t += 1; i += 1; } while(j <= right) { temp[t] = arr[j]; j += 1; t += 1; } //3.将临时数组放入原数组中 int index = left; int k = 0; while(k < t) { arr[index] = temp[k]; k += 1; index += 1; } } }
7、基数排序
基本介绍:基数排序用到了桶排序的思想,将数据的同一位进行比较,然后放入对应的桶中,再逐个取出数据。
基本思想:先创建十个桶,每个桶代表着一个数位上的数字,将所有数组数据长度设置为最大数位的值,在数组中取出同一个数位上的数字进行入桶操作,然后再逐个取出来,
分别从低位到高位进行入桶、出桶,最终就会得到有序的数组。

时间复杂度:O(n*logn) 800万 不到1s
代码实现:
public static void radixSort(int[] arr) { //获取最大数的位数 int max = 0; for(int i = 0;i < arr.length; i++) { if(max < arr[i]) { max = arr[i]; } } int maxLength = (max + "").length(); //建立桶子 二维数组 int [][] tong =new int[10][arr.length]; //建立每个桶子的数的个数 int[] inNumber = new int[10]; //执行操作 for(int i = 0,n = 1; i < maxLength; i++,n*=10) { //入桶,求出每个元素的位值,然后入桶 for(int j = 0 ; j < arr.length; j++) { int digOfElement = (arr[j] / n) % 10; tong[digOfElement][inNumber[digOfElement]] = arr[j]; inNumber[digOfElement]++;//忘了移动索引 } int index = 0; //出桶 for(int k = 0; k < inNumber.length; k++) { if(inNumber[k] != 0) { //放值 for(int l = 0; l < inNumber[k]; l++) { arr[index++] = tong[k][l]; } } inNumber[k] = 0; } }
8、堆排序
基本介绍:堆排序用到的是线性二叉数组,也属于选择排序的一种。
基本思想:先将数组调整成为一个大顶堆,然后将顶元素与最后一个元素位置交换,数组长度减一。将交换后的数组继续调整成为新的大顶堆,并再次进行交换,以此类推。

时间复杂度: O(n*logn) 800万数据不到 1s完成。
代码实现:
//编写一个堆排序 public static void heapSort(int[] arr) { System.out.println("堆排序!!"); int temp = 0; //最终代码: //1.先弄一个大顶堆,升序 for(int i = arr.length / 2 + 1; i >= 0; i--) { adjustHeap(arr, i, arr.length); } //2,交换大顶堆和最后一个元素,长度减一 //3,在剩下的数组中调整大顶堆。 for(int j = arr.length - 1; j > 0; j--) { temp = arr[j]; arr[j] = arr[0]; arr[0] = temp; adjustHeap(arr, 0, j); } } //将一个数组(二叉树),调整成一个大顶堆 /** * * @param arr[] 待调整的数组 * @param i 表示非叶子节点再数组中的索引 * @param length 表示当前数组中还有多少待调整的元素 */ public static void adjustHeap(int arr[], int i, int length) { //先取出当前元素的值 int temp = arr[i]; //开始调整 for(int k = i * 2 + 1; k < length; k = k * 2 + 1) { //从左右子节点中找到最大的那个值的索引 if(k + 1 < length && arr[k] < arr[k + 1]) { k++; } //如果子节点大于父节点,直接交换 if(arr[k] > temp) { arr[i] = arr[k]; i = k;//i 指向最大的元素k,继续循环比较 }else { break;//我们是从左到右,从下到上,不必判断左下层子节点 } } //当for循环结束后,已经将以i为父节点的局部的树变成大顶堆。 arr[i] = temp;//将temp值放到调整后的位置。 }
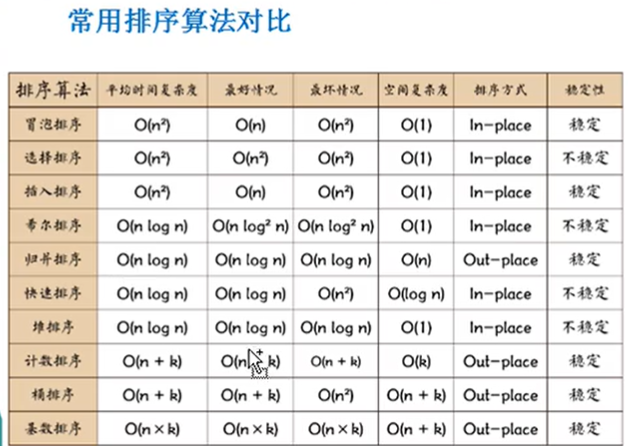
1、稳定:如果a原先再b前面,而a=b,排序之后a仍然在b的前面;
不稳定:如果a原先再b前面,而a=b,排序之后a可能会出现在b的后面;
2、内排序:所有排序操作都在内存中进行
外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行
3、时间复杂度:一个算法执行所耗费的时间。
4、空间复杂度:运行一个程序所需内存的大小。
5、n: 数据规模;k:"桶的个数"。
6、In-place: 不占用额外内存;
Out-place:占用额外内存。
原文转载:http://www.shaoqun.com/a/494499.html
白色清关:https://www.ikjzd.com/w/1410
华翰物流:https://www.ikjzd.com/w/1799
zozotown:https://www.ikjzd.com/w/2180
个人学习、研究八大经典排序 1、冒泡排序基本介绍:冒泡排序是一种交换排序基本思想:(假定从小到大的顺序)从第一个元素开始,相邻两个数据进行比较,将小的值放在左边。第一轮:从第一个元素开始,和与其相邻的后一个元素进行比较, 若后一个比前一个小,则交换位置,否则不变,然后两个索引都向后移动一位,继续判断至最后一组数据,第二轮:从第二个元素出发,继续重复上述进行比较、换位,
阿里巴巴 批发:阿里巴巴 批发
tenso:tenso
澳门有什么好吃的?:澳门有什么好吃的?
旅行结婚 跟着明星度蜜月:旅行结婚 跟着明星度蜜月
广州长隆六一活动一览表?长隆六一儿童节优惠政策有哪些?:广州长隆六一活动一览表?长隆六一儿童节优惠政策有哪些?
No comments:
Post a Comment